Over-Dispersion: How sure are you?

“Precision (certainty) is important in making decisions” is a statement that I have little uncertainty that even the most disagreeable of people will accept. But how often do you check that your estimated uncertainty is consistent with your observed uncertainty?

A common barrier is that for GLMs it may not be clear what the model predicted variance should be. Which is why as always your selfless author has taken it upon him self to explain (i.e., I talk too much about things that no one else cares about for the gratification of my ego).

For example Fig. 1 shows histograms of two sets of quiz scores. The means of both sets are indistinguishable from their true mean of 5, however the variances are 21.30 and 2.72 respectively. The variance of a binomial is ; for and the variance should be 2.5, thus the first has a much higher observed variance then theoretical variance.

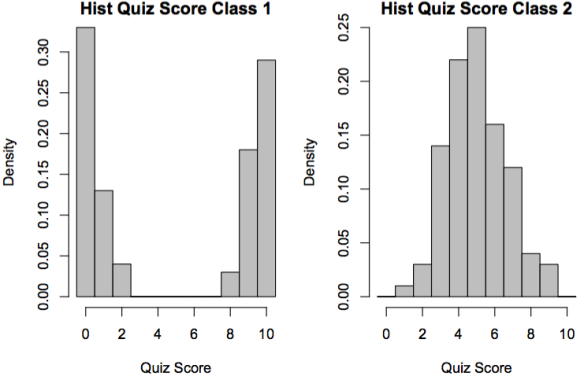
Histograms of Quiz scores for two classes of 100 students. The means are 4.97 and 5.01; the standard deviations are 4.62 and 1.65 for the two classes respectively.

The ratio of the theoretical variance to the observed variance is called dispersion (). If then the model is over-dispersed; if  then the model is under-dispersed.  This post will consider only over-dispersion. Over-dispersion is evidence that there are missing explanatory variables.

In the quiz example there are clearly two groups in class 1 but they are modeled as only one group. Thus the best way to model over-dispersed data is to find the missing underling predictor however in general this might not be possible (or desirable if a simple uni-variate relationship is sought). The non-Bayesian way (i.e., inferior way) to handle dispersion is to use a quasi-likelihood GLM (Prof. Altman class is where I learned about this in my under grad and I still refer to her excellent notes; If you are reading this Dr Altman please convert your notes into a text book). To summarize this method, the log likelihood is replaced with a score function () that has the same properties (,  , and ) used to derive the asymptotic results in exponential family GLM modeling. Here is the number of observations, is the model parameter, and is the data uncertainty. The parameters are then estimated optimizing instead of likelihood.

This method has the advantage that it can be implement in r with only a few extra key strokes:

“glm(cbind(Correct,Wrong  )~factor(Class), data=data.example, family=binomial(link=”probit”) )”

is the normal way and

“glm(cbind(Correct,Wrong  )~factor(Class), data=data.example, family=quasibinomial(link=”probit”) )”

is the quasi likelihood way. The down side is that quasi likelihood is not likelihood and consequently can not be used in many Bayesian model selection schemes (e.g., there is no evidence estimate or even BIC for quasi-likelihood models).

The Bayesian way (i.e., the correct way) is to use a prior distribution with non stated hyper parameters () to give the model the flexibility to account for dispersion. The “recipe” is to make . For the quiz example this means using a binomial distribution for and a beta distribution for the result of the integral is then the beta binomial distribution, though if you don’t want to take wiki’s word for it, this is a fun integral to work though in a pretentious coffee shop on a rain day. Particularly if you are trying to pull an attractive 3rd math student; the functions give it a pleasantly complex appearance. In other words, the beta binomial distribution is the product of a binomial distribution with a beta prior having the probability of a success integrated out. Conceptually this means that the probability of a success is random from a beta distribution; unknown predictors are then absorbed into this distribution.

The pdf of beta binomial is where is the probability of a success and is precision. For a GLM it would be normal to define (the function would typically be either a probit or logit) and estimate on its own. This is analogous to estimating the mean and sd for a linear regression.

The appended code gives an example of estimating the probability of success answering a question for both class with 4 additional confounding parameters. A classic binomial GLM is also run. For the GLM, most simulated data sets (about 80% but I have not conducted an exhaustive simulation) find at least one confounding parameters to be a significant predictor of probability of success. The GLM summary for one run is

“Call:
glm(formula = cbind(k, n – k) ~ ., family = binomial(link = “logit”),
    data = X)

Deviance Residuals:
    Min       1Q   Median       3Q      Max  
-4.0594  -2.1550  -0.1402   2.1930   4.4550  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.137667   0.126606   1.087 0.276875    
V1          -0.235301   0.181677  -1.295 0.195264    
V2          -0.177382   0.085473  -2.075 0.037959 *  
V3           0.078763   0.090477   0.871 0.384009    
V4           0.351333   0.102759   3.419 0.000629 ***
V5           0.001959   0.092348   0.021 0.983073    
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 381.54  on 59  degrees of freedom
Residual deviance: 366.40  on 54  degrees of freedom
AIC: 478.64

Number of Fisher Scoring iterations: 4″

The result of the Beta Binomial model is

The parameter estimates with standard errors and 95 percent central credibility intervals (denoted by their lower and upper bounds, LB and UB).

The Beta binomial model correctly does not find any of the parameters to be significantly different from zero.

Code:
g.beta.binomial <- function(x, n, mu=0.5, phy=1000, Log.out =T )
{
#print(is.numeric(n))
#print(is.numeric(x))
#print(is.numeric(phy))
#print(is.numeric(mu))
#temp=data.frame(A1 = x+phy*mu, B1 = n-x+phy*(1-mu), A2 = phy*mu, B2= phy*(1-mu))
#print(temp)
#LP = lbeta(temp$A1, temp$B1)-lbeta( phy*mu, phy*(1-mu))+lchoose(n, x)

LP = lbeta(x+phy*mu, n-x+phy*(1-mu))-lbeta( phy*mu, phy*(1-mu))+lchoose(n, x)
if(Log.out == F) {LP = exp(LP)}

LP[is.nan(LP)] = -300 # get NaNs out

LP = sum(LP)

#print(LP)

return(LP)
}
g.LL <- function(M, K, n, X, npar, ndat) # the log likelihood
{
eta = 0*(1:ndat) + M[2] # the systimatic part
#print(is.numeric(eta))
for (i in 1:npar)
{
#print(is.numeric(M[2+i]))
#print(is.numeric(X[,i]))
eta = eta + M[2+i]*X[,i]
#print(is.numeric(eta))
}
Mu = 1/(1+exp(-eta)) # the expected value

Phy = M[npar+3]
#print(K)
#print(n)

LL = g.beta.binomial(K, n, mu=Mu, phy=Phy, Log.out =T )

return(LL)
}

# does not do rotation
g.BBstep <- function(M, k., n., X., Q.sd., npar., ndat.)
{

# int step
new = M
new[2] = new[2] + Q.sd.[1]*rnorm(1)
new[1] = g.LL(new, k., n., X., npar., ndat.)
r = runif(1)
A = exp(new[1]-M[1])
if (is.na(A)) {A= 0}
if (A>=r)
{
M = new
}
# the model pars
for (i in 1:npar.)
{
j = i + 2
new = M
new[j] = new[j] + Q.sd.[i+1]*rnorm(1)
new[1] = g.LL(new, k., n., X., npar., ndat.)
r = runif(1)
A = exp(new[1]-M[1])
if (is.na(A)) {A= 0}
if (A>=r)
{
M = new
}
}
# int step
new = M
new[npar.+3] = new[npar.+3] + Q.sd.[npar.+2]*rnorm(1)
if(new[npar.+3] > 0)
{new[1] = g.LL(new, k., n., X., npar., ndat.)
r = runif(1)
A = exp(new[1]-M[1])
if (is.na(A)) {A= 0}
if (A>=r)
{
M = new
}
}
return(M)
}
g.BB.glm <- function(k, n, X, NSTEPS = 50000, nsave = 1000)
{
npar = ncol(X) # get the number of pars
ndat = length(k)
parnames = colnames(X) # par names
old = (1:(npar+3))*0 # LL, intersept, pars, dispersion

# this gets the starting model and step size
MOD.start = glm(cbind(k, n-k)~., data=X, family = binomial(link = “logit”))
print(summary(MOD.start))
old[1] = -Inf
old[2:(npar+2)] = MOD.start$coefficients # staring model
old[npar+3] = 100*sum(n) # starting dispersion

Q.sd = sqrt(diag(vcov(MOD.start))) # step size
Q.sd = c(Q.sd, sum(n))
print(Q.sd)
# fixed length thinning
par.buf = matrix(0, nrow=nsave, ncol=(npar+1+1+1+1)) # the saved models pars
# this part samples and saves the models
print(date())
burn= 10000
for (i in 1:(nsave+burn)) # loop over sampling first
{
old = g.BBstep(old, k, n, X, Q.sd.=Q.sd, npar, ndat) # new model (1 swweep) with LL

#print(old)
if (i >= burn +1)
{
j = i – burn
par.buf.temp = c(j, old)
#print(par.buf.temp)
#print(par.buf[i,])
par.buf[j,] = par.buf.temp
#print(par.buf[i,])
}
}

print(date())
for (i in 3:(ncol(par.buf)))
{
Q.sd[i-2] = sd(par.buf[,i])
}
Q.sd[length(Q.sd)] = Q.sd[length(Q.sd)]
print(cor(par.buf[,3:ncol(par.buf)]))
print(Q.sd)

alpha = 1 # start flt
for (i in 1:NSTEPS) # loop over sampling first
{
old = g.BBstep(old, k, n, X, Q.sd.=Q.sd, npar, ndat) # new model with LL
# flt
ori = sample(1:nsave, 1) # the model that gets writen over
alpha = (alpha*nsave)/(alpha+nsave) # prob current model
r = runif(1) # random value

if (r <= alpha)
{
par.buf.temp = c(i+nsave, old)
par.buf[ori,] = par.buf.temp
}

}

phy = par.buf[,ncol(par.buf)]
rho = (sum(n)+phy)/(phy+1)

rownames(par.buf) = 1:nsave
#print(par.buf)

par.buf = cbind(par.buf, rho)
index.s = sort.int(par.buf[,1],index.return = TRUE)
#print(index.s)
par.buf = par.buf[index.s$ix,]

#print(par.buf)

M.list = 3:(ncol(par.buf))
SD.list = 3:(ncol(par.buf))
LB.list = 3:(ncol(par.buf))
UB.list = 3:(ncol(par.buf))

for (i in 3:(ncol(par.buf)))
{
j = i-2
M.list[j] = mean(par.buf[,i])
SD.list[j] = sd(par.buf[,i])
LB.list[j] = quantile(par.buf[,i], prob=0.025)
UB.list[j] = quantile(par.buf[,i], prob=0.975)
}
tab = data.frame(Estimate = M.list, SD = SD.list, LB = LB.list, UB = UB.list)
rownames(tab) = c(“Intercept”, colnames(X), “Psi”, “Rho”)

print(round(tab, 4))

print(round(cor(par.buf[,3:9]),4))
par(mfrow=c(1,2))

plot(par.buf[,1], phy, xlab=”Index”, ylab=”Percision”)
#quartz()
plot(par.buf[,1], rho, xlab=”Index”, ylab=”Dispersion”)

#breaks.rho = seq(1, 1.01*max(rho), length.out=201)
#h1=hist(rho, breaks=breaks.rho, plot =F)
#plot(h1$den,, h1$mids, type=”n”, xaxs=”i”, yaxs=”i”)
#polygon( c(0, h1$den, 0), c(min(h1$mids), h1$mids, max(h1$mids)), col=”grey”)
}

g.BB.glm(c(rbinom(15, size =10, prob = 0.05), rbinom(15, size =10, prob = 0.95),rbinom(30, size =10, prob = 0.5) ),
rep(10, 20),
X=as.data.frame(matrix(c(rep(0,30), rep(1,30), rnorm(60*4)), nrow=60, ncol=5)))

What does that look like? The output